Direct Variation (also known as Direct Proportion)
The concept of direct variation is summarized by the equation below.
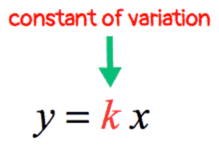
We say that [latex]y[/latex] varies directly with [latex]x[/latex] if [latex]y[/latex] is expressed as the product of some constant number [latex]k[/latex] and [latex]x[/latex].
If we isolate [latex]k[/latex] on one side, it reveals that [latex]k[/latex] is the constant ratio between [latex]y[/latex] and [latex]x[/latex]. In other words, dividing [latex]y[/latex] by [latex]x[/latex] always yields a constant output.
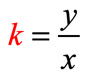
[latex]k[/latex] is also known as the constant of variation, or constant of proportionality.
Examples of Direct Variation
Example 1: Tell whether [latex]y[/latex] varies directly with [latex]x[/latex] in the table below. If yes, write an equation to represent the direct variation.
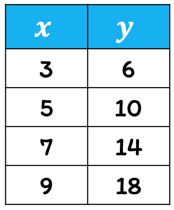
Solution:
To show that [latex]y[/latex] varies directly with [latex]x[/latex], we need to verify if dividing [latex]y[/latex] by [latex]x[/latex] always gives us the same value.

Since we always arrived at the same value of [latex]2[/latex] when dividing [latex]y[/latex] by [latex]x[/latex], we can claim that [latex]y[/latex] varies directly with [latex]x[/latex]. This constant number is, in fact, our [latex]k = 2[/latex].
To write the equation of direct variation, we replace the letter [latex]k[/latex] by the number [latex]2[/latex] in the equation [latex]y = kx[/latex].
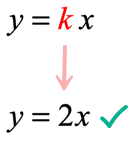
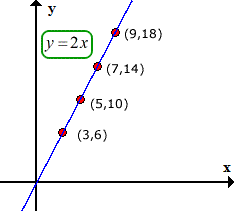
When an equation that represents direct variation is graphed in the Cartesian Plane, it is always a straight line passing through the origin.
Think of it as the Slope-Intercept Form of a line written as
[latex]y = mx + b[/latex] where [latex]b = 0[/latex]
Here is the graph of the equation we found above.
Example 2: Tell whether [latex]y[/latex] varies directly with [latex]x[/latex] in the table below. If yes, write an equation to represent direct variation.
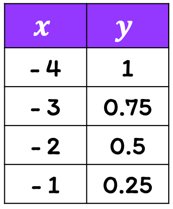
Solution:
Divide each value of [latex]y[/latex] by the corresponding value of [latex]x[/latex].
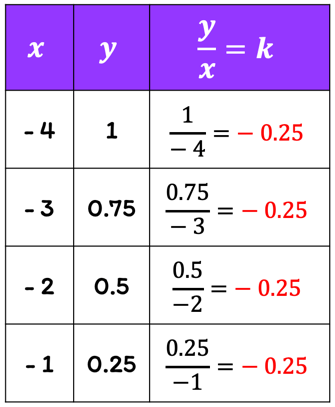
The quotient of [latex]y[/latex] and [latex]x[/latex] is always [latex]k = – \,0.25[/latex]. That means [latex]y[/latex] varies directly with [latex]x[/latex]. Here is the equation that represents its direct variation.
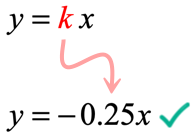
Here is the graph. Having a negative value of [latex]k[/latex] implies that the line has a negative slope. As you can see, the line is decreasing from left to right.
In addition, since [latex]k[/latex] is negative we see that when [latex]x[/latex] increases the value of [latex]y[/latex] decreases.
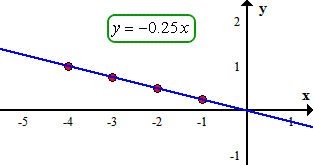
Example 3: Tell whether if [latex]y[/latex] directly varies with [latex]x[/latex] in the table. If yes, write the equation that shows direct variation.
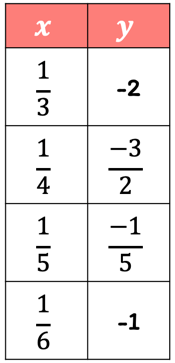
Solution:
Find the ratio of [latex]y[/latex] and [latex]x[/latex], and see if we can get a common answer which we will call constant [latex]k[/latex].
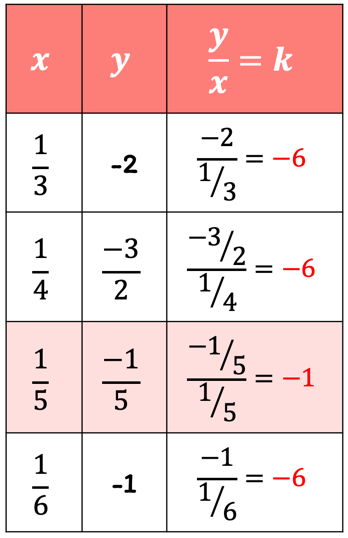
It looks like the [latex]k[/latex]-value on the third row is different from the rest. In order for it to be a direct variation, they should all have the same [latex]k[/latex]-value.
The table does not represent direct variation, therefore, we can’t write the equation for direct variation.
Example 4: Given that [latex]y[/latex] varies directly with [latex]x[/latex]. If [latex]x = 12[/latex] then [latex]y = 8[/latex].
- Write the equation of direct variation that relates [latex]x[/latex] and [latex]y[/latex].
- What is the value of [latex]y[/latex] when [latex]x = – \,9[/latex]?
a) Write the equation of direct variation that relates [latex]x[/latex] and [latex]y[/latex].
Since [latex]y[/latex] directly varies with [latex]x[/latex], I would immediately write down the formula so I can see what’s going on.
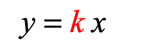
We are given the information that when [latex]x = 12[/latex] then [latex]y = 8[/latex]. Substitute the values of [latex]x[/latex] and [latex]y[/latex] in the formula and solve [latex]k[/latex].
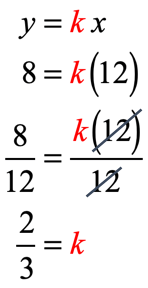
Replace the “[latex]k[/latex]” in the formula by the value solved above to get the direct variation equation that relates [latex]x[/latex] and [latex]y[/latex].
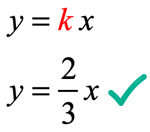
b) What is the value of [latex]y[/latex] when [latex]x = – \,9[/latex]?
To solve for [latex]y[/latex], substitute [latex]x = – \,9[/latex] in the equation found in part a).
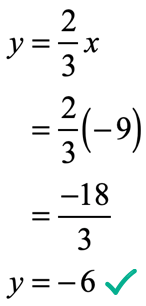
Example 5: If [latex]y[/latex] varies directly with [latex]x[/latex], find the missing value of [latex]x[/latex] in

Solution:
We will use the first point to find the constant of proportionality [latex]k[/latex] and to set up the equation [latex]y = kx[/latex].
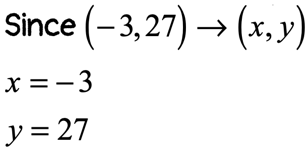
Substitute the values of [latex]x[/latex] and [latex]y[/latex] to solve for [latex]k[/latex].
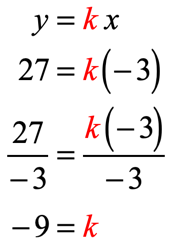
The equation of direct proportionality that relates [latex]x[/latex] and [latex]y[/latex] is…
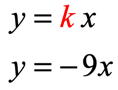
We can now solve for [latex]x[/latex] in ([latex]x[/latex], [latex] – \,18[/latex]) by plugging in [latex]y = – \,18[/latex].
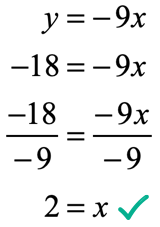
Example 6: The circumference of a circle ([latex]C[/latex]) varies directly with its diameter. If a circle with the diameter of [latex]31.4[/latex] inches has a radius of [latex]5[/latex] inches,
- Write the equation of direct variation that relates the circumference and diameter of a circle.
- What is the diameter of the circle with a radius of [latex]7[/latex] inches?
a) Write the equation of direct variation that relates the circumference and diameter of a circle.
We don’t have to use the formula [latex]y = k\,x[/latex] all the time. But we can use it to come up with a similar set-up depending on what the problem is asking.
The problem tells us that the circumference of a circle varies directly with its diameter, we can write the following equation of direct proportionality instead.
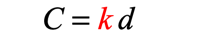
The diameter is not provided but the radius is. Since the radius is given as [latex]5[/latex] inches, that means, we can find the diameter because it is equal to twice the length of the radius. This gives us [latex]10[/latex] inches for the diameter.
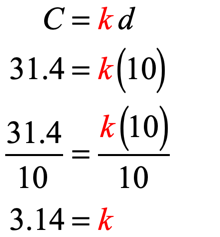
The equation of direct proportionality that relates circumference and diameter is shown below. Notice, [latex]k[/latex] is replaced by the numerical value [latex]3.14[/latex].
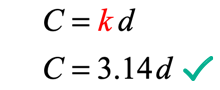
b) What is the diameter of a circle with a radius of [latex]7[/latex] inches?
Since the equation requires diameter and not the radius, we need to convert first the value of radius to diameter. Remember that diameter is twice the measure of a radius, thus [latex]7[/latex] inches of the
Now, we substitute [latex]d = 14[/latex] into the formula to get the answer for circumference.
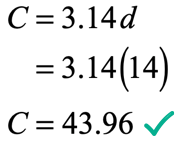
You may also be interested in these related math lessons or tutorials:
